三角函数,神奇的函数
目录
什么是三角函数
三角函数
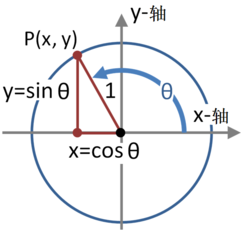
三角函数单位圆
在单位圆中,用三角形的三条边的比例来定义三角函数的各各关系。
| 正弦 | 余弦 | 正切 | 余切 | 正割 | 余割 |
|---|---|---|---|---|---|
| \(\sin \theta = y\) | \(\cos \theta = x\) | \(\tan \theta = \frac{y}{x}\) | \(\cot \theta = \frac{x}{y}\) | \(\sec \theta = \frac{1}{x}\) | \(\csc \theta = \frac{1}{y}\) |
反三角函数
反三角函数是三角函数的逆函数
| 反三角函数 | 三角函数 | 定义域 | 值域 |
|---|---|---|---|
| \(y = \arcsin(x)\) | \(x = \sin(y)\) | \(-1 \leq x \leq 1\) | \(-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}\) |
| \(y = \arccos(x)\) | \(x = \cos(y)\) | \(-1 \leq x \leq 1\) | \(0 \leq y \leq \pi\) |
| \(y = \arctan(x)\) | \(x = \tan(y)\) | \(-\infty < x < +\infty\) | \(-\frac{\pi}{2} < y < \frac{\pi}{2}\) |
| \(y = \text{arccot}(x)\) | \(x = \cot(y)\) | \(-\infty < x < +\infty\) | \(0 < y < \pi\) |
| \(y = \text{arcsec}(x)\) | \(x = \sec(y)\) | \(x \leq -1 \text{ or } 1 \leq x\) | \(0 \leq y < \frac{\pi}{2} \text{ or } \frac{\pi}{2} < y \leq \pi\) |
| \(y = \text{arccsc}(x)\) | \(x = \csc(y)\) | \(x \leq -1 \text{ or } 1 \leq x\) | \(-\frac{\pi}{2} \leq y < 0 \text{ or } 0 < y \leq \frac{\pi}{2}\) |
什么是三角公式表
平方和公式
\[\begin{equation}\sin^2x+\cos^2x=1\end{equation}\] \[\begin{equation}1+\tan^2x=sec^2x\end{equation}\] \[\begin{equation}1+\cot^2x=csc^2x\end{equation}\]和角公式
\[\begin{equation} \sin(\alpha + \beta) = \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta) \end{equation}\] \[\begin{equation} \cos(\alpha + \beta) = \cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta) \end{equation}\] \[\begin{equation} \tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha)\tan(\beta)} \end{equation}\]差角公式
\[\begin{equation} \sin(\alpha - \beta) = \sin(\alpha)\cos(\beta) - \cos(\alpha)\sin(\beta) \end{equation}\] \[\begin{equation} \cos(\alpha - \beta) = \cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta) \end{equation}\] \[\begin{equation} \tan(\alpha - \beta) = \frac{\tan(\alpha) - \tan(\beta)}{1 + \tan(\alpha)\tan(\beta)} \end{equation}\]和差化积公式
\[\begin{equation} \sin(\alpha) + \sin(\beta) = 2\sin\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha - \beta}{2}\right) \end{equation}\] \[\begin{equation} \sin(\alpha) - \sin(\beta) = 2\cos\left(\frac{\alpha + \beta}{2}\right)\sin\left(\frac{\alpha - \beta}{2}\right) \end{equation}\] \[\begin{equation} \cos(\alpha) + \cos(\beta) = 2\cos\left(\frac{\alpha + \beta}{2}\right)\cos\left(\frac{\alpha - \beta}{2}\right) \end{equation}\] \[\begin{equation} \cos(\alpha) - \cos(\beta) = -2\sin\left(\frac{\alpha + \beta}{2}\right)\sin\left(\frac{\alpha - \beta}{2}\right) \end{equation}\]诱导公式
奇变偶不变,符号看象限
| 公式 | 一 | 二 | 三 | 四 | 五 | 六 |
|---|---|---|---|---|---|---|
| 角 | \(2k\pi+\alpha(k\equiv Z)\) | \(\pi+\alpha\) | \(-\alpha\) | \(\pi-\alpha\) | \(\frac{\pi}{2}-\alpha\) | \(\frac{\pi}{2}+\alpha\) |
| 正弦 | \(\sin \alpha\) | \(-\sin \alpha\) | \(-\sin \alpha\) | \(\sin \alpha\) | \(\cos \alpha\) | \(\cos \alpha\) |
| 余弦 | \(\cos \alpha\) | \(-\cos \alpha\) | \(\cos \alpha\) | \(-\cos \alpha\) | \(\sin \alpha\) | \(-\sin \alpha\) |
| 正切 | \(\tan \alpha\) | \(\tan \alpha\) | \(-\tan \alpha\) | \(-\tan \alpha\) | ||
| 口诀 | 奇变偶不变,符号看象限 |
记背诀窍:奇变偶不变,符号看象限,即形如(2k+1)90°±α,则函数名称变为余名函 数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。形如2k×90°±α,则函数名称不变。
欧克拉公式
\[\begin{equation} e^{ix} = \cos(x) + i\sin(x) \end{equation}\]傅里叶变化中的应用
正交函数集
- 正交性:集合中的任意两个不同函数的内积(通常是积分)为零。
- 完备性:如果这组函数能够通过线性组合表示定义域内的任意函数,则称其为完备正交函数集。(没有不在这个集合内的其他的函数符合这个关系)
我们把这个三角函数集合称之为完备正交函数集 在区间 [−π,π]上,三角函数集{1,cos(nx),sin(nx)∣n=1,2,3,…}
因为
参考资料
文档信息
- 本文作者:Kingdmzhen
- 本文链接:https://icci.ink/2025/04/06/math-%E4%B8%89%E8%A7%92%E5%87%BD%E6%95%B0%E5%90%88%E9%9B%86/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)
